Petri-Netze: Definition, Erklärung und Eigenschaften

Den Ursprung und letztendlich auch ihren Namen haben die Petrinetze aus der Dissertationsschrift „Kommunikation mit Automaten“ von Carl Adam Petri. Waren Petrinetze gerade am Anfang aber eher noch Betrachtungsgegenstand von Theoretikern erfolgte der Übergang in die Praxis erst Mitte der 1980er Jahre. Nachfolgend werden Petrinetze näher vorgestellt und erläutert.

Mathematische Darstellung eines Petrinetzes

In der einfachsten Form lässt sich ein Petrinetz, bzw. eine entsprechender Netzgraph eines Petrinetzes, durch das Triple N = (S,T,F) darstellen, mit:

• S = Stellen
• T = Transitionen
• F = Flussrelation

Diese mathematische Darstellung eines Petrinetzes lässt sich zusätzlich noch um eine Anfangsmarkierung (m₀) und eine Kantentgewichtung (W) zu N = (S, T, F, W, m⁰) ergänzen.
Stellen und Transitionen sind die Netzelemente eines Petrinetzes. Jedes Element besitzt eine Vorbereich und einen Nachbereich, wobei der Vorbereich eines Netzelements x die Menge aller Eingangsknoten von X ist und der Nachbereich des Elements X die Menge aller Ausgangsknoten von x.

Vorteile und Nachteile von klassischen Petrinetze

Nachfolgend einige Vorteile und Nachteile von einfachen Petrinetzen:

Vorteile

• Formelle Syntax
• Einfach zu verstehen
• Gute Analysemöglichkeiten
• Hersteller unabhängig

Nachteilen

• Modelle können groß und komplex werden
• Modelle werden schnell unüberschaubar
• Zeit, Kosten und Daten können nicht modelliert werden

Erreichbarkeitsgraph/Markierungsgraph

Mit Hilfe eines Erreichbarkeitsgraph (bzw. auch Markierungsgraph genannt), kann man ausgehend von einer Startmarkierung verfolgen, welche anschließende Folgemarkierung davon möglich sind. Über den Markeriungsgraph lassen sich bestimmte Eigenschaften eines Petri-Netzes, z.B. ob Soundness vorliegt, relativ schnell beantworten. Auch ob ein Petri-Netz terminiert, lässt sich mit einen Blick vom Markierungsgraph ablesen. Dies ist nämlich dann der Fall, wenn der Markierungsgraph zyklenfrei ist.

Petri-Netz Eigenschaften

Nachfolgend findet man einige Eigenschaften von Petri-Netzen aufgeführt und kompakt, teilweise auch mit Beispiel, erklärt.

Tot

Von einer toten Transition unter einer Markierung m spricht man, wenn keine Folgemarkierung diese Transition aktivieren kann.

Eine Markierung bezeichnet man hingegen als tot, wenn alle Transitionen tot sind.

Lebendig

Eine Transition nennt man lebendig unter einer Markierung m, wenn sie unter keiner Folgemarkierung m‘ tot ist.
Analog nennt man eine Markierung lebendig, wenn alle Transitionen lebendig sind.

Verklemmungsfrei

Nicht ganz so streng nimmt es die Eigenschaft Verklemmungsfrei. Man nennt nämliche eine Markierung verklemmungsfrei, wenn keine tote Markierung erreichbar ist.

Sollte der Markierungsgraph keinen Knoten ohne Nachfolge haben, dann ist das Netz verklemmungsfrei.

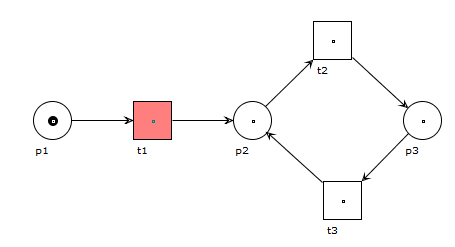
Terminiert

Ist die Menge der Schaltfolgen eines markierten Petrinetzes endlich, dann terminiert das Petrinetz. Hat der Markierungsgraph keine Zyklen, dann ist das der Beweis, dass das Netz terminiert.

Beschränkt

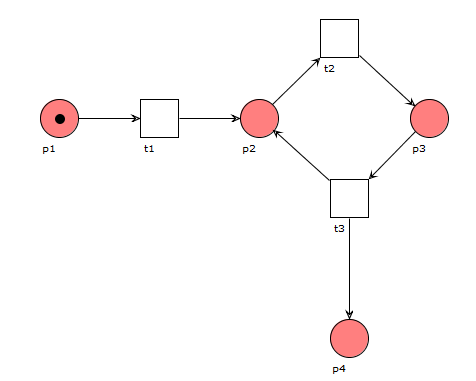
Bleibt die Anzahl der Marken in einem Petrinetz während der Laufzeit gleich, dann kann man von einem beschränkten Netz sprechen. Generell gilt ein Petrinetz als beschränkt, falls nicht unendlich viele Token erzeugt werden können.

Reversibel

Von einem reversiblen Netz spricht man, wenn die Startmarkierung m₀ von jeder anderen erreichbaren Markierung aus erreichbar ist.

Soundness

Ein Petri-Netz gilt als intakt (sound), wenn folgende drei Eigenschaften erfüllt sind:

1. Für jede Markierung die in die Startstelle gelegt wird, muss es möglich sein, dass eine Markierung in der Endstelle entsteht
2. Falls die Markierung die Endstelle erreicht, darf keine andere Stelle im Netz markiert sein
3. Es darf keine tote Transitionen geben, alle Transitionen müssen vom initialen Zustand in einen Zustand kommen, in dem die Transition schalten kann

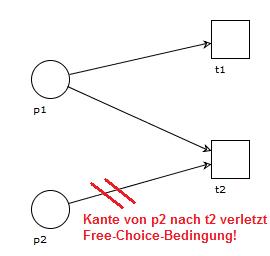
Free-Choice-Netz

Bei einem Free-Choice-Netz dürfen Transitionen einer vorwärts verzeigten Stelle nicht rückwärts verzweigt sein. Die Transitionen sind damit nur von der beteiligten Stelle abhängig und es kann „frei gewählt“ werden, welche Transition nun schalten soll. Es gibt also keine weitere Vorbedingung, die Wahl ist frei.

High-Level-Petrinetze

Aus den oben dargestellten Nachteilen von klassischen Petrinetzen sind die sogenannten High-Level-Petrinetze entstanden. Diese bieten beispielsweise unterscheidbaren Marken (auch: gefärbte Marken, colored tokens). Ebenfalls können Zeitaspekte in High-Level-Petrinetzen modelliert werden. Zu guter Letzt können auch noch Hierarchien abgebildet werden, in dem man ein Netzelement durch ein entsprechend berandetes Teilnetz ersetzt (Subnetz).

Ähnliche Themen:

• YAWL – Yet Another Workflow Language: Vorstellung und Erklärung
• Druckerfunktionen erklärt
• Mehr Tempo mit Vectoring: VDSL Beine gemacht
• N24 Internet Stick Erfahrungsbericht
• Alles über DSL – Anfang, Anwendung und Angebote